PERCOBAAN DIFRAKSI SINAR-X

A. Tujuan Percobaan

Tujuan dari percobaan ini yaitu :

1. Mempelajari karakteristik radiasi sinar-x.

2. Mempelajari pengaruh tegangan terhadap intensitas sinar-x terdifraksi.

3. Mempelajari sifat difraksi sinar-x pada kristal.

4. Menentukan parameter kisi kristal padatan (KBr).

B. Teori Dasar

Ditemukan oleh Wilhelm Roentgen (1895), radiasi sinar-x dihasilkan saat elektron penembak yang bergerak dipercepat menumbuk permukaan suatu bahan padat (logam). Semakin cepat gerak elektron, semakin besar sinar-x yang dihasilkan. Semakin banyak jumlah elektron, semakin besar intensitas sinar-x. Jika sebuah elektron bebas bergerak dipercepat sehingga mampu menerobos suatu atom hingga membentuk elektron pada kulit terdalam hingga keluar. Karena adanya kekosongan pada kulit terdalam, maka untuk mempertahankan keadaan stabil, elektron terluar akan mengisi kekosongan pada kulit atom terdalam sambil memancarkan gelombang sinar-x.

Menurut terori elektromagnetik, sinar-x juga dapat dihasilkan melalui peristiwa pengereman elektron yang dipercepat yang disebut peristiwa Bremsstrahlung. Sinar-x memiliki daya tembus yang cukup besar dan panjang gelombangnya berorde 10⁻¹⁰ m yang bersesuaian dengan ukuran kisi kristal. Karena itu, sinar-x dapat digunakan untuk menganalisis struktur kristal bahan padatan melalui peristiwa difraksi. Peristiwa difraksi sinar-x pada kristal padatan dinyatakan dengan persamaan Bragg :

Dengan dhkl adalah jarak antar bidang kristal, 𝜃 adalah sudut difraksi, 𝜆 adalah panjang gelombang, dan n = 1, 2, 3, ....

Jarak antar bidang kristal sejajar yang berdekatan merupakan fungsi dari indeks Miller (hkl) dan tetapan kisi (a). Untuk struktur kristal kubus dapat ditulis :

Dengan s = h² + k² + l². Jika s diketahui maka nilai h, k, dan l akan diperoleh. Struktur kristal berbeda akan menunjukkan kumpulan nilai s yang berbeda pula. Untuk struktur kristal sistem kubus, nilai kumpulan s ditunjukkan sebaga berikut :

Kubus sederhana : 1, 2, 3, 4, 5, 6, 8, 9, 10, ...

Kubus pusat badan (bcc) : 2, 4, 6, 8, 10, 12, 14, ...

Kubus pusat muka (fcc) : 3, 4, 8, 11, 12, 16, ...

C. Alat dan Bahan

Alat dan bahan yang digunakan pada Percobaan Difraski Sinar-x :

1. Satu set peralatan difraksi sinar-x.

2. Sumber tegangan.

3. Sampel KBr.

D. Prosedur Percobaan

Berikut ini prosedur pada Percobaan Difraksi Sinar-x :

1. Menyusun dan menyiapkan peralatan difraksi sinar-x dengan posisi sumber sinar-x, sampel, dan detektor adalah sejajar (𝜃 = 0).

2. Mengatur besar tegangan 15 kV.

3. Mencatat besar intensitas sinar-x terhadap sudut 2𝜃 mulai dari 5° hingga 90° dengan waktu cacah 10 s.

4. Mengulangi percobaan untuk tegangan 20 kV.

E. Data Percobaan

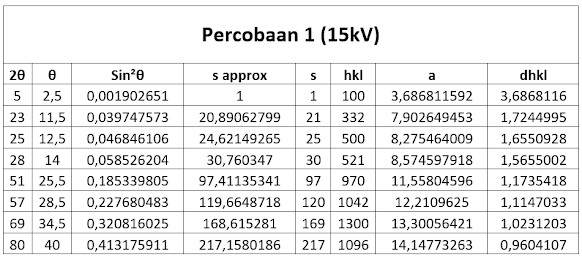
Untuk V = 15 kV

Untuk V = 20 kV

F. Pengolahan dan Perhitungan Data

                                V = 15 kV                                                            V = 20 kV

G. Analisa Data

Pada percobaan ini digunakan sudut 2𝜃, bukanlah 𝜃 karena jika sudut 𝜃 terlalu kecil maka sudut difraksi pada percobaan tidak akan terukur secara teratur. Pada percobaan ini digunakan sudut 2𝜃 mulai dari 5° hingga 90°, baik untuk tegangan 15 kV dan 20 kV.  Pada percobaan dapat dilihat bahwa semakin besar tegangan, maka intensitas yang diperoleh akan semakin besar. Baik pada percobaan I dan II, nilai intensitas bervariasi (naik-turun) pada sudut tertentu. Hal ini karena dalam spektrum kontinyu sinar-x timbul akibat adanya pengereman-pengereman elektron yang memiliki energi kinetik tinggi pada anoda. Pada saat pengereman, sebagian energi diubah menjadi sinar-x. Pengereman elektron ini dapat terjadi tiba-tiba. Akibatnya, intensitas yang terbentuk berubah-ubah karena energinya juga berubah-ubah.

Untuk nilai s pada percobaan mengikuti pola kubus pusat muka (fcc). Pada kubus ini, atom-atom berada pada setiap sudut kubus dan setiap sudut bidang. Dari hasil percobaan bahwa semakin besar nilai s, maka tetapan kisi yang diperoleh semakin besar. Begitupula dengan nilai dhkl, semakin kecil nilai s dan semakin besar a, maka nilai dhkl akan semakin besar.

Pada intensitas maksimum tertentu dan pda sudut tertentu, diambil titik-titik pertemuan agar dapat melihat titik maksimumnya. Dari literatur bahwa nilai a = 6,41 - 6,5 Å, sedangkan dari percobaan diperoleh nilai a = 3,68 - 14,14 Å. Dari literatur dhkl = 3 Å, sedangkan dari percobaan diperoleh nilai dhkl = 0,96 - 3,68 Å. Penyimpangan kemungkinan terjadi saat pergantian sudut tiap 1° kurang tepat dan tidak mereset ulang hasil intensitas. Jika dibandingkan intensitas sinar-x terdifraksi oleh KBr dan tabung sinar-x, maka nilai intensitas terdifraksi oleh KBr akan memiliki nilai intensitas yang lebih kecil. Hal ini disebabkan adanya hamburan dan penyerapan berkas oleh atom dalam medium. Sedangkan, pada tabung sinar-x, tegangan yang tinggi akan menghasilkan intensitas yang besar jika tidak ada proses pengereman elektron.

H. Kesimpulan dan Saran

Dalam percobaan ini dapat disimpulkan sebagai berikut.

1. Radiasi sinar-x dihasilkan saat elektron penembak yang bergerak dipercepat menumbuk permukaan suatu bahan padat (logam).

2. Semakin besar tegangan, maka nilai intensitas sinar-x terdifraksi akan semakin besar.

3. Sinar-x dapat digunakan untuk menganalisis struktur kristal bahan padatan melalui peristiwa difraksi.

4. Struktur kristal KBr yaitu kubus pusat muka (fcc). Kisi padatan KBr bergantung pada nilai s, 𝜆², dan sin²𝜃. Dari percobaan, nilai tetapan kisi (a) yang diperoleh yaitu kisaran 3,68 - 14,14 Å.

Dalam percobaan ini dapat disarankan sebagai berikut.

1. Tidak lupa mereset alat setiap kali mengambil data.

2. Tidak membuka tabung kaca setelah tabung dialiri tegangan.

I. Daftar Pustaka

Arthur Beiser. (1995). Concept of Modern Physics, 5th edition, New York: McGraw Hill.

Cullity, B.D. (1978). Elements of x-ray diffraction, 2nd ed. New York: Addison Wesley.

Phywe manual catalogue. Characteristic x-ray and Bragg scattering with higher order. LEP 5.4.01

Phywe manual catalogue. Characteristic x-ray of copper. LEP 5.4.01

Raymond A. Serway, Clement J. Moses and Curt A Moyer. (2005). Modern Physics, 3 rd edition, Belmont: Thomson Learning, Inc.

CONTOH SOAL FISIKA DASAR : HUKUM NEWTON TENTANG GERAK

1. Tuliskan Hukum Newton tentang gerak.

Jawab :

Hukum I Newton : "Setiap benda akan diam atau bergerak lurus beraturan jika resultan gaya yang bekerja pada benda itu sama dengan nol".

ΣF = 0

ΣFx = 0 ; ΣFy = 0

Hukum II Newton : "Percepatan suatu benda yang disebabkan oleh suatu gaya sebanding dan searah dengan gaya itu dan berbanding terbalik dengan massa benda yang dikenai oleh gaya tersebut".

ΣF = ma

Hukum III Newton : "Besar gaya aksi dan reaksi pada dua benda yang berbeda selalu sama besar tetapi berlawanan arah".

FA = -FR

2. Bola tenis yang massanya 60 g mendekati raket dengan kelajuan 30 m/s, bersentuhan dengan raket selama 5 ms, kemudian terpantul kembali dengan kelajuan yang sama. Tentukan gaya rata-rata raket yang bekerja pada bola tersebut.

3. Gaya horizontal sebesar 10 N dikerjakan pada balok bermassa 4 kg yang diam di atas bidang datar yang licin. Tentukan kelajuan balok dan berapa jarak yang ditempuh balok setelah 6 s ?

4. Sebuah lift yang massa totalnya 800 kg tergantung pada kabel yang tegangan maksimumnya 20.000 N. Berapakah percepatan maksimum yang diizinkan agar kabel tidak putus ?

5. Sebuah balok yang massanya 100 kg berada di atas bidang datar yang kasar. Jika koefisien gesekan statis dan kinetis antara balok dan bidang masing-masing 𝜇s = 0,5 dan 𝜇k = 0,4. Tentukan : 

a. Gaya minimum yang diperlukan untuk menggerakkan balok.

b. Gaya minimum yang diperlukan untuk menjaga balok bergerak dengan kelajuan konstan.

c. Percepatan benda bila balok ditarik dengan gaya sebesar 500 N.

6. Sebuah rak buku bermassa 100 kg terletak pada bidang miring yang kasar. Jika koefisien gesekan antara rak buku dan bidang adalah 0,3 dan 0,5. Tentukan :

a. Sudut kemiringan bidang agar rak buku bergerak dengan kelajuan tetap.

b. Gaya minimum untuk memulai gerakan pada sudut kemiringan tersebut.

7. Sebuah elektron bergerak mengelilingi inti atom dengan lintasan berbentuk lingkaran yang jari-jarinya 5,29 x 10⁻¹¹ m. Bila kecepatan elektron 2,19 x 10⁶ m/s dan massanya 9,1 x 10⁻³¹ kg, berapa gaya sentripetal yang dialami elektron ?

8. Massa sebuah sepeda dan pengendaranya sama dengan 100 kg. Sepeda tersebut akan melintas di suatu jalan miring yang jari-jari lintasannya sama dengan 30 m. Bila kelajuan sepeda adalah 16 m/s, tentukan :

a. Percepatan sentripetal sepeda.

b. Sudut kemiringan jalan (g = 10 m/s²).

9. Sebuah pesawat bergerak dengan kelajuan 480 km/jam. Ketika akan mendarat, pilot memiringkan pesawatnya sebesar 45° sehingga akhirnya pesawat berbelok. Berapakah jari-jari belokan pesawat ini ? 

10. Seseorang yang massanya 50 kg berada dalam sebuah lift. Lift bergerak dengan percepatan 5 m/s²  (g = 10 m/s²). Hitung gaya tekan normal orang terhadap lift bila :

a. Lift dipercepat ke atas.

b. Lift dipercepat ke bawah.

CONTOH SOAL FISIKA DASAR : HUKUM NEWTON TENTANG GRAVITASI

1. Jelaskan Hukum Newton tentang Gravitasi.

Jawab :

Hukum Gravitasi Universal Newton yaitu setiap dua benda di dunia ini mengalami gaya tarik-menarik yang besarnya berbanding lurus dengan massa masing-masing benda dan berbanding terbalik dengan kuadrat jarak antara keduanya.

Besar gaya gravitasi dapat dituliskan dalam bentuk persamaan :

2. Jelaskan definisi medan gravitasi dan kuat medan gravitasi.

Jawab :

Medan gravitasi adalah ruang di sekitar benda bermassa yang masih dipengaruhi gaya gravitasi benda tersebut. Kuat medan gravitasi adalah gaya gravitasi tiap satu satuan massa yang dialami benda pada suatu titik tertentu. Secara matematis ditulis :

3. Jika jari-jari bumi adalah 6.400 km, masa bumi 6 x 10²⁴ kg, dan konstanta gravitasi universal 6,67 x 10⁻¹¹ Nm²/kg². Tentukan kuat medan gravitasi di permukaan bumi.

4. Jika diketahui jarak rata-rata antara planet Merkurius dengan matahari adalah 0,4 kali jarak rata-rata bumi - matahari. Periode bumi mengitari matahari adalah 1 tahun, berapa tahun periode Merkurius mengitari matahari ?

5. Jika jari-jari bumi R = 6,4 x 10⁶ m dan percepatan gravitasi di permukaan bumi 9,8 m/s². Jika ada sebuah satelit yang mengorbit pada ketinggian R dari permukaan bumi, maka berapa kecepatan linear satelit tersebut agar :

a. Satelit tetap mengorbit.

b. Satelit keluar dari orbitnya dan meninggalkan bumi.

c. Satelit keluar dari orbitnya dan jatuh ke bumi.

6. Dua buah benda langit masing-masing bermassa 1.000 kg mula-mula dalam keadaan diam dan terpisah pada jarak 10 m. Tentukan percepatan awal kedua benda tersebut. (G = 6,67 x 10⁻¹¹ Nm²/kg²).

7. Bumi mempunyai massa 5,97 x 10²⁴ kg dan jari-jarinya 6,37 x 10⁶ m, Sebuah benda massanya 2 kg berada di permukaan bumi. Berapakah besar gaya gravitasi yang dialami oleh benda tersebut ?

8. Bila percepatan gravitasi di permukaan bumi 9,8 m/s², tentukanlah percepatan gravitasi pada ketinggian R di atas permukaan bumi dimana R = jari-jari bumi.

9. Percepatan gravitasi di permukaan bumi adalah 10 m/s² dan jari-jari bumi R. Berapa besar kecepatan awal yang harus diberikan pada sebuah benda yang ditembakkan vertikal ke atas dari permukaan bumi agar benda sampai ke angkasa ?

10. Bila massa bumi 5,97 x 10²⁴ kg dan jari-jari bumi 6.370 km dan bumi dianggap berbentuk bola padat. Hitunglah rapat jenis bumi.

CONTOH SOAL FISIKA DASAR : TERMODINAMIKA

1. Tentukan jumlah kalor yang diperlukan untuk memanaskan 4 mol gas helium dari 0°C hingga 100°C pada volume tetap.

2. Tentukan efisiensi (daya guna) dari suatu mesin yang bekerja pada reservoir suhu rendah 47°C dan reservoir suhu tinggi 527°C.

3. Sebuah mesin turbo jet reservoir pembakarannya bersuhu 1.727°C dan reservoir suhu rendahnya di dalam tempat pembuangan gas 527°C. Untuk menghasilkan usaha sebesar 2 x 10⁷ J diperlukan kalor pembakaran sebesar 8 x 10⁷ J. Tentukan.

a. Efisiensi Carnot idealnya.

b. Efisiensi sesungguhnya dari mesin ini.

4. Sejumlah kalor sebesar 3.000 J ditambahkan ke sistem dan dilakukan kerja 2.000 J pada sistem. Berapa besar perubahan energi dalam sistem tersebut ?

5. Jika reservoir suhu tinggi 800 K maka efisiensi maksimum mesin 40%. Agar efisiensi maksimumnya naik menjadi 50%, maka harus berapakah suhu pada reservoir tinggi ?

6. Suhu tinggi reserboir mesin Carnot 500 K dan efisiensinya 60%. Agar efisiensi mesin Carnot menjadi 80%, maka harus berapakah suhu tinggi reservoir mesin Carnot tersebut ?

7. Sebuah mesin Carnot bekerja diantara dua reservoir panas 487°C dan reservoir dingin 107°C. Jika mesin tersebut menyerap kalor 800 J dari reservoir panas, maka berapa jumlah kalor yang dibuang dari mesin ?

8. Tentukan efisiensi dari suatu mesin yang bekerja pada reservoir suhu rendah 7°C dan reservoir suhu tinggi 427°C.

9. Mesin Carnot bekerja diantara dua buah reservoir suhu tinggi 222°C dan suhu rendah 2°C. Berapa usaha yang dihasilkan oleh mesin itu jika kalor yang diperlukan 1.200 J ?

10. Suatu tabung tertutup yang volumenya 600 liter berisi gas bertekanan 6 atm. Hitunglah usaha yang dilakukan jika :

a. Gas memuai pada tekanan tetap sehingga volumenya menjadi 3x volume semula.

b. Gas dimampatkan pada tekanan tetap sehingga volumenya menjadi 1/2x volume semula.

11. Suatu gas pada tekanan konstan 8,1 x 10⁴ Pa dimampatkan dari 9 liter menjadi 2 liter. Dalam proses tersebut, gas melepas kalor sebesar 400 J. Tentukan.

a. Usaha yang dilakukan oleh gas.

b. Perubahan energi dalam.

12. Suatu gas dalam ruang tertutup menerima kalor sebanyak 7.000 kalori dan menghasilkan usaha sebesar 7.000 J. Berapa peruabahan energi dalam gas ?

13. Sebuah mesin Carnot yang menggunakan reservoir suhu tinggi 727°C mempunyai efisiensi 30%. Tentukan suhu dari reservoir rendahnya.

CONTOH SOAL FISIKA DASAR : BESARAN DAN SATUAN

1. Sebutkan definisi besaran dan satuan.

Jawab :

Besaran adalah sesuatu yang dapat diukur dan dinyatakan dengan angka-angka. Sedangkan satuan adalah sesuatu yang menyertai nilai suatu besaran. Sebagai contoh yaitu panjang seutas tali 25 m, artinya panjang merupakan suatu besaran, 25 merupakan ukuran panjang, dan m merupakan suatu satuan.

2. Sebutkan besaran-besaran dalam Fisika.

Jawab :

a. Besaran pokok

Besaran pokok adalah besaran yang satuannya sudah ditentukan (ditetapkan) secara internasional. Dalam fisika terdapat 7 besaran pokok, yaitu :

b. Besaran Turunan

Besaran turunan adalah besaran yang diturunkan dari satu atau beberapa besaran pokok. Beberapa besaran turunan yaitu :

c. Besaran Skalar

Besaran skalar adalah besaran yang mempunyai nilai saja. Yang termasuk besaran skalar adalah semua besaran pokok, luas, volume, massa jenis, energi, daya, dan sebagainya. Contoh :

- Panjang tali 30 cm.

- Massa benda 4 kg.

- Waktu tempuh 10 menit.

d. Besaran vektor

Besaran vektor adalah besaran yang mempunyai nilai dan arah. Yang termasuk besaran vektor adalah perpindahan, kecepatan, percepatan, gaya, momentum, momen gaya, dan sebagainya. Contoh :

- Mobil bergerak dengan kecepatan 50 km/jam ke barat.

- Benda didorong dengan gaya 15 N ke kiri.

- Budi berpindah 4 m ke depan.

3. Tuliskan dimensi besaran pokok dan besaran turunan.

Jawab :

Dimensi adalah cara penyusunan suatu besaran yang diberi kurung besar "( )" atau kurung persegi "[ ]".

4. Tuliskan aturan penulisan notasi ilmiah.

Jawab :

Notasi ilmiah dituliskan dalam bentuk rumusan :

Aturan penulisan dengan notasi ilmiah :

a. Untuk bilangan lebih dari 10, pindahkan desimal ke kiri dengan eksponen bertanda positif. Contoh :

- 75.000 ditulis 7,5 x 10⁴

- 123.000 ditulis 1,23 x 10⁵

- Massa bumi yaitu 5,97 x 10²⁴ kg

b. Untuk bilangan kurang dari 1, pindahkan desima ke kanan dengan eksponen bertanda negatif. Contoh :

- 0,0024 ditulis 2,4 x 10⁻³

- 0,0765 ditulis 7,65 x 10⁻²

5. Sebutkan sifat-sifat vektor.

Jawab :

- Dapat dipindahkan asal besar dan arah tidak berubah.

- Dapat dijumlahkan.

- Dapat dikurangkan.

- Dapat diuraikan.

- Dapat dikalikan.

6. Dua buah vektor dengan kecepatan v1 = 6 m/s dan v2 = 10 m/s melalui satu titik tangkap dengan sudut apit 60°. Hitunglah resultan vektornya.

Jawab :

7. Sebuah gaya sebesar 40 N bekerja dengan membentuk sudut 60° terhadap sumbu horizontal. Hitung komponen vektor pada sumbu-x dan sumbu-y.

Jawab :

Fx = F cos 30° = 40 . ½√3 = 20 √3 N 

Fy = F sin 30° = 40 . ½ = 20 N

8. Hitunglah hasil perkalian titik antara dua vektor berikut ini.

P = i + 2j - 3k dan Q = 4i - 5j + 6k

Jawab :

P ᐧ Q = (1)(4) + (2)(-5) + (-3)(6) = 4 - 10 - 18

P ᐧ Q = -24

9. Hitunglah hasil perkalian silang antara dua vektor berikut ini.

P = i + 3j + 5k dan Q = 2i + 4j + 6k

Jawab :

P ⨯ Q = (PyQz - PzQy)i + (PzQx - PxQz)j + (PxQy - PyQx) k

P ⨯ Q = [(3)(6) - (5)(4)]i + [(5)(2) - (1)(6)]j + [(1)(4) - (3)(2)]k

P ⨯ Q =[18 - 20]i + [10 - 6]j + [4-6]k

P ⨯ Q = -2i + 4j -2k

10. Sebutkan definisi angka penting dan ketentuannya.

Jawab :

Angka penting adalah angka-angka hasil pengukuran yang terdiri dari angka-angka pasti dan angka taksiran. Ketentuan mengenai angka penting yaitu :

a. Semua angka bukan nol adalah angka penting.

Contoh : 431,5 cm mengandung 4 angka penting (yaitu 4, 3, 1, dan 5).

b. Angka nol yang terletak diantara angka bukan nol termasuk angka penting.

Contoh : 81,002 kg mengandung 5 angka penting (yaitu 8, 1, 0, 0, dan 2).

c. Angka nol di sebelah kanan angka bukan nol adalah angka penting.

Contoh : 8.200 gram mengandung 4 angka penting (yaitu 8, 2, 0, dan 0).

d. Angka nol di sebelah kiri angka bukan nol, tetapi tidak didahului angka bukan nol, tidak termasuk angka penting.

Contoh : 0,0026 kg mengandung 2 angka penting (yaitu 2 dan 6).

11. Tentukan banyaknya angka penting.

Jawab :

a. 2,500 x 10⁴ cm → mengandung 4 angka penting (yaitu 2, 5, 0, dan 0).

b. 7,0001 inci → mengandung 5 angka penting (yaitu 7, 0, 0, 0, dan 1).

c. 3,02 x 10³ kg → mengandung 3 angka penting (yaitu 3, 0, dan 2).

d. 6,620 x 10⁻² m → mengandung 4 angka penting (yaitu 6, 6, 2, dan 0).

12. Jika 𝜋 = 3,14159 hitunglah :

a. Keliling dan luas lingkaran yang jari-jarinya 2,5 m

b. Volume tabung yang jari-jarinya 0,50 m dan tingginya 3,5 m

Jawab :

𝜋 = 3,14159 bukan angka penting karena bukan hasil pengukuran.

a. Keliling dan luas lingkaran

r = 2,50 m → mengandung 3 angka penting (yaitu 2, 5, dan 0).

K = 2𝜋r = 2 (3,14159)(2,50)

K = 15,7 m → mengandung 3 angka penting (yaitu 1, 5, dan 7).

L = 𝜋r² = (3,14159)(2,50)²

L = 19,6 m² → mengandung 3 angka penting (yaitu 1, 9, dan 6).

b. Volume tabung

r = 0,50 m → mengandung 2 angka penting (yaitu 5 dan 0).

t = 3,5 m → mengandung 2 angka penting (yaitu 3 dan 5).

V = 𝜋r²t = (3,14159)(0,50)²(3,5)

V = 2,8 m³ → mengandung 2 angka penting (yaitu 2 dan 8).