1. Sebutkan definisi besaran dan satuan.
Jawab :
Besaran adalah sesuatu yang dapat diukur dan dinyatakan dengan angka-angka. Sedangkan satuan adalah sesuatu yang menyertai nilai suatu besaran. Sebagai contoh yaitu panjang seutas tali 25 m, artinya panjang merupakan suatu besaran, 25 merupakan ukuran panjang, dan m merupakan suatu satuan.
2. Sebutkan besaran-besaran dalam Fisika.
Jawab :
a. Besaran pokok
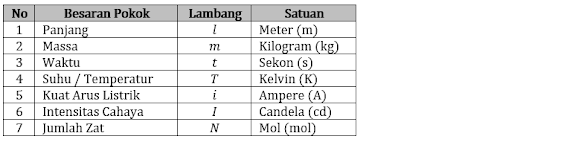
Besaran pokok adalah besaran yang satuannya sudah ditentukan (ditetapkan) secara internasional. Dalam fisika terdapat 7 besaran pokok, yaitu :
b. Besaran Turunan
Besaran turunan adalah besaran yang diturunkan dari satu atau beberapa besaran pokok. Beberapa besaran turunan yaitu :
c. Besaran Skalar
Besaran skalar adalah besaran yang mempunyai nilai saja. Yang termasuk besaran skalar adalah semua besaran pokok, luas, volume, massa jenis, energi, daya, dan sebagainya. Contoh :
- Panjang tali 30 cm.
- Massa benda 4 kg.
- Waktu tempuh 10 menit.
d. Besaran vektor
Besaran vektor adalah besaran yang mempunyai nilai dan arah. Yang termasuk besaran vektor adalah perpindahan, kecepatan, percepatan, gaya, momentum, momen gaya, dan sebagainya. Contoh :
- Mobil bergerak dengan kecepatan 50 km/jam ke barat.
- Benda didorong dengan gaya 15 N ke kiri.
- Budi berpindah 4 m ke depan.
3. Tuliskan dimensi besaran pokok dan besaran turunan.
Jawab :
Dimensi adalah cara penyusunan suatu besaran yang diberi kurung besar "( )" atau kurung persegi "[ ]".
4. Tuliskan aturan penulisan notasi ilmiah.
Jawab :
Notasi ilmiah dituliskan dalam bentuk rumusan :
Aturan penulisan dengan notasi ilmiah :
a. Untuk bilangan lebih dari 10, pindahkan desimal ke kiri dengan eksponen bertanda positif. Contoh :
- 75.000 ditulis 7,5 x 10⁴
- 123.000 ditulis 1,23 x 10⁵
- Massa bumi yaitu 5,97 x 10²⁴ kg
b. Untuk bilangan kurang dari 1, pindahkan desima ke kanan dengan eksponen bertanda negatif. Contoh :
- 0,0024 ditulis 2,4 x 10⁻³
- 0,0765 ditulis 7,65 x 10⁻²
5. Sebutkan sifat-sifat vektor.
Jawab :
- Dapat dipindahkan asal besar dan arah tidak berubah.
- Dapat dijumlahkan.
- Dapat dikurangkan.
- Dapat diuraikan.
- Dapat dikalikan.
6. Dua buah vektor dengan kecepatan v1 = 6 m/s dan v2 = 10 m/s melalui satu titik tangkap dengan sudut apit 60°. Hitunglah resultan vektornya.
Jawab :
7. Sebuah gaya sebesar 40 N bekerja dengan membentuk sudut 60° terhadap sumbu horizontal. Hitung komponen vektor pada sumbu-x dan sumbu-y.
Jawab :
Fx = F cos 30° = 40 . ½√3 = 20 √3 N
Fy = F sin 30° = 40 . ½ = 20 N
8. Hitunglah hasil perkalian titik antara dua vektor berikut ini.
P = i + 2j - 3k dan Q = 4i - 5j + 6k
Jawab :
P ᐧ Q = (1)(4) + (2)(-5) + (-3)(6) = 4 - 10 - 18
P ᐧ Q = -24
9. Hitunglah hasil perkalian silang antara dua vektor berikut ini.
P = i + 3j + 5k dan Q = 2i + 4j + 6k
Jawab :
P ⨯ Q = (PyQz - PzQy)i + (PzQx - PxQz)j + (PxQy - PyQx) k
P ⨯ Q = [(3)(6) - (5)(4)]i + [(5)(2) - (1)(6)]j + [(1)(4) - (3)(2)]k
P ⨯ Q =[18 - 20]i + [10 - 6]j + [4-6]k
P ⨯ Q = -2i + 4j -2k
10. Sebutkan definisi angka penting dan ketentuannya.
Jawab :
Angka penting adalah angka-angka hasil pengukuran yang terdiri dari angka-angka pasti dan angka taksiran. Ketentuan mengenai angka penting yaitu :
a. Semua angka bukan nol adalah angka penting.
Contoh : 431,5 cm mengandung 4 angka penting (yaitu 4, 3, 1, dan 5).
b. Angka nol yang terletak diantara angka bukan nol termasuk angka penting.
Contoh : 81,002 kg mengandung 5 angka penting (yaitu 8, 1, 0, 0, dan 2).
c. Angka nol di sebelah kanan angka bukan nol adalah angka penting.
Contoh : 8.200 gram mengandung 4 angka penting (yaitu 8, 2, 0, dan 0).
d. Angka nol di sebelah kiri angka bukan nol, tetapi tidak didahului angka bukan nol, tidak termasuk angka penting.
Contoh : 0,0026 kg mengandung 2 angka penting (yaitu 2 dan 6).
11. Tentukan banyaknya angka penting.
Jawab :
a. 2,500 x 10⁴ cm → mengandung 4 angka penting (yaitu 2, 5, 0, dan 0).
b. 7,0001 inci → mengandung 5 angka penting (yaitu 7, 0, 0, 0, dan 1).
c. 3,02 x 10³ kg → mengandung 3 angka penting (yaitu 3, 0, dan 2).
d. 6,620 x 10⁻² m → mengandung 4 angka penting (yaitu 6, 6, 2, dan 0).
12. Jika 𝜋 = 3,14159 hitunglah :
a. Keliling dan luas lingkaran yang jari-jarinya 2,5 m
b. Volume tabung yang jari-jarinya 0,50 m dan tingginya 3,5 m
Jawab :
𝜋 = 3,14159 bukan angka penting karena bukan hasil pengukuran.
a. Keliling dan luas lingkaran
r = 2,50 m → mengandung 3 angka penting (yaitu 2, 5, dan 0).
K = 2𝜋r = 2 (3,14159)(2,50)
K = 15,7 m → mengandung 3 angka penting (yaitu 1, 5, dan 7).
L = 𝜋r² = (3,14159)(2,50)²
L = 19,6 m² → mengandung 3 angka penting (yaitu 1, 9, dan 6).
b. Volume tabung
r = 0,50 m → mengandung 2 angka penting (yaitu 5 dan 0).
t = 3,5 m → mengandung 2 angka penting (yaitu 3 dan 5).
V = 𝜋r²t = (3,14159)(0,50)²(3,5)
V = 2,8 m³ → mengandung 2 angka penting (yaitu 2 dan 8).














No comments:
Post a Comment